பிராச்சிஸ்டோக்ரோன் புதிர்

பத்ரி சேஷாத்ரி

அந்த காலக் கணித மேதைகளிடம் தமக்குள்ளாகப் புதிர் போட்டு விடுவித்துக்கொள்வது வாடிக்கையாக இருந்தது. அதன்மூலமாக கணிதம் பெரும் பாய்ச்சலையும் செய்தது. அதில் ஒன்றுதான் மேலே தலைப்பில் நீங்கள் பார்க்கும் வாய்க்கு வழங்காத பெயர்.

இதை முதலில் தமிழாக்கிவிடுவோம். ‘பிராச்சிஸ்டோ’ என்றால் ‘மிகக் குறைவான’ என்று பொருள். ‘க்ரோன்’ என்றால் ‘நேரம்’. ஆக, கடமுடவென்று இருக்கும் ‘பிராச்சிஸ்டோக்ரோன்’ என்றால் ‘மிகக் குறைவான நேரம்’ என்பதுதான் பொருள்.

புவி ஈர்ப்பு விசையால் ஒரு பொருள் கீழ் நோக்கி இழுக்கப்படும் என்பது உங்களுக்குத் தெரியும். இந்தப் புவி ஈர்ப்பு விசையால் இழுக்கப்பட்டு, ஒரு புள்ளியிலிருந்து இன்னொரு புள்ளிக்கு ஒரு பொருள் வந்துசேர, எந்தப் பாதையில் பயணித்தால் அது எடுத்துக்கொள்ளும் நேரம் மிகக் குறைவாக இருக்கும்? இதுதான் இந்த புதிர்.

இன்னும் கொஞ்சம் கவனமாக இந்த புதிரைப் பார்ப்போம். வெறும் காற்றில் ஒரு பொருள் விழுகிறது என்றால் அது நீங்கள் நினைத்த இடத்துக்கெல்லாம் போகாது. எனவே, ஓரிடத்திலிருந்து இன்னோர் இடத்துக்கு ஒரு பொருளைத் தள்ளவேண்டும் என்றால், அதற்கு என நாம் ஒரு பாதையை உருவாக்கி வைத்திருக்கவேண்டும். அந்தப் பாதையில் பொருள் வழுக்கிக்கொண்டு அல்லது உருண்டுகொண்டு, சரிந்துகொண்டு விழவேண்டும்.

இந்த படத்தில் A, B என்ற இந்த இரு புள்ளிகளை எடுத்துக்கொண்டால், இவை இரண்டையும் இணைக்கும் கோடுகள் எண்ணற்ற பல. மிக எளிதான நேர் கோடு ஒன்று. இரண்டையும் இணைக்கக்கூடிய வட்டங்கள் என்று எடுத்துக்கொண்டாலே அவை மட்டுமே முடிவிலி (இன்ஃபினிடி). இப்படி கணக்கற்ற பல வடிவங்கள் இருக்கும்போது எந்தக் கோடு வழியே வந்தால் ‘A’-யிலிருந்து வரும் ஒரு பொருள் ‘B’–க்கு மிக வேகமாக வந்துசேரும்?

பெரும்பாலானவர்கள், இதற்கான விடை ‘நேர்கோடு’ என்று சட்டென்று சொல்லிவிடுவார்கள். இரு புள்ளிகளை இணைக்கும் குறைவான நீளம் கொண்ட பாதை நேர்கோடுதானே? ஆனால், நாம் இங்கு பேசுவது அது இல்லை. இன்னொருமுறை குறைவான நீளம் கொண்ட பாதைகளைப் பார்ப்போம்.

இங்கு நாம் பார்ப்பது மிகக் குறைவான நேரம் எடுக்கும் பாதையை. அது நேர்கோடு இல்லை என்று மட்டும் சொல்லிவிட்டால் போதுமா?

சரி, இப்படியெல்லாம் ரூம் போட்டு உட்கார்ந்து யார் முதலில் யோசித்தது?

கலீலியோ கலீலி என்பவரைப் பற்றி தெரியுமல்லவா? பூமிதான் சூரியனைச் சுற்றுகிறது என்று சொல்லி சர்ச்சிடம் வாங்கிக் கட்டிக்கொண்டவர். அக்காலத்தின் தன்னிகரற்ற விஞ்ஞானி. இவர், 16ஆம் நூற்றாண்டின் இறுதியில் தன் எழுத்துகளில் இதனைக் குறிப்பிட்டிருந்தார். இவரது சமகாலத்தவர் இத்தாலியரான கைடோபால்டோ டெல் மாண்டி. கலீலியோவும் டெல் மாண்டியும் கடிதப் பரிமாற்றம் வைத்துக் கொண்டிருந்தனர். அந்தக் கடிதங்கள் மூலமாக ‘பிராச்சிஸ்டோக்ரோன் புதிர்’ பற்றி இருவரும் தகவல்களை பரிமாறிக்கொண்டனர். 1588ஆம் ஆண்டிலேயே கலீலியோ இதைப் பற்றி பேசியிருந்தார் என்பது தெரியவருகிறது.

உள்ளுணர்வின் வழியாகவும் பல பரிசோதனைகள் மூலமாகவும் கலீலியோ இந்தப் புதிரைப் பரிசோதித்து வந்தார். ஒரு கட்டத்தில், இந்த இரு புள்ளிகளையும் இணைக்கும் வட்டத்தின் ஒரு பகுதியாக அந்த வடிவம் இருக்குமா என்று கேட்டுப் பார்த்தார். பின்னர், இதையெல்லாம் தீர்க்க வேறு உயர்கணித முறை வேண்டும் என்று விட்டுவிட்டார்.

கலீலியோவுக்குப் பிறகு வந்தவர்கள்தான் ஐஸக் நியூட்டனும் கோட்ஃப்ரெட் லீபினிட்ஸும். இவர்கள்தான் ‘கால்குலஸ்’ என்ற நுண்கணிதத்தை கண்டுபிடித்தனர். அதன் காரணமாகக் கடுமையாகச் சண்டையிட்டுக் கொண்டனர். லீபினிட்ஸிடமிருந்துதான் பெர்னோலி குடும்பத்தைச் சேர்ந்த பலரும் கால்குலஸை கற்றுக்கொண்டனர்.

இப்படி கால்குலஸை கற்றுக்கொண்ட யோஹான் பெர்னோலி, கலீலியோவின் புதிருக்கு வந்து சேர்ந்தார். இப்போது அதைத் தீர்ப்பதற்கான கருவி அவரிடம் இருந்தது. போட்டு பார்த்தார். அவருக்கு ஒரு விடை கிடைத்துவிட்டது. ஒரே குஷி அவருக்கு.

ஜூன் 1696இல் (கலீலியோ இந்தப் புதிரைப் பற்றிப் பேசி சுமார் 100 ஆண்டுகள் கழித்து), யோஹான் பெர்னோலி இந்தப் புதிரை ஒரு கணித ஆராய்ச்சி இதழில் வெளியிட்டார். நியூட்டன், லீபினிட்ஸ் இருவருமே அதைப் பார்ப்பார்கள் என்பது அவருக்குத் தெரியும். அவருடைய சகோதரர் யாக்கோப் பெர்னோலியும் அதனைப் பார்ப்பார் என்று அவருக்குத் தெரியும். தான் கண்டுபிடித்த விடையை அவர்களால் கண்டுபிடிக்க முடியுமா?

மே 1697இல் யோஹான் பெர்னோலி இதற்கான விடையை வெளியிட்டார். அவருடைய விடை சரியானதுதான் என்றாலும் அவர் அதைத் தருவித்த முறையில் சில தவறுகள் இருந்தன. ஐந்து பேராளுமைகள் உடனே பதில் எழுதினர். யார் யார்?

1. நியூட்டன் (தன் பெயரை மறைத்து, புனைபெயரில்)
2. லீபினிட்ஸ்
3. யாக்கோப் பெர்னோலி
4. எஹ்ரன்ஃப்ரீட் ஃபான் ஷிர்னாஸ்
5. கில்லாம் தி லாப்பித்தால்

யாக்கோப் பெர்னோலிக்கும் யோஹான் பெர்னோலிக்குமான போட்டி சாதாரணமானதல்ல. இருவரும் பல காரணங்களுக்காக ஒருவரை ஒருவர் கடுமையாக வெறுத்தனர். தன் சகோதரனைவிடத் தானொரு படி மேலே போக முயற்சித்த யாக்கோப், ‘கால்குலஸ் ஆஃப் வேரியேஷன்ஸ்’ என்ற ஒரு புதிய துறையையே உருவாக்கினார்.

கால்குலஸை புரிந்துகொள்ள நாம் பின்னர் ஒருமுறை முயற்சி செய்வோம். இப்போது, இந்த புதிருக்கான விடைக்கு வருவோம்.

சின்னப் பையனாக இருக்கும்போது நாமெல்லாம் டயர் ஓட்டுவோமே, ஞாபகம் இருக்கிறதா? சைக்கிள் டயரை மட்டும் வைத்துக்கொள்ளாமல், ரிம்முடன் சேர்ந்த டயராக வைத்துக்கொள்ளுங்கள். அந்த டயரின் மேல்பாகத்தில் கருப்பாக ஒரு புள்ளியைக் குறித்துக்கொள்ளுங்கள். ஒருவர் டயரை ஓட்டும்போது நீங்கள் தள்ளி உட்கார்ந்துகொண்டு அந்தப் புள்ளி எப்படியெல்லாம் நகருகிறது என்பதை மட்டும் பாருங்கள். அந்தப் புள்ளி இப்படித்தான் போகும்.

மேலே உள்ளதில் சிறிய வட்டம்தான் டயர். வளைந்து வளைந்து செல்லும் கோடு ஒன்று தெரிகிறதே, அதற்கு பெயர் சைக்ளாய்ட்.

இந்த சைக்ளாய்ட் என்னும் வடிவம் சில ஆயிரம் ஆண்டுகளுக்கு முன்னதாகவே நன்கு தெரிந்திருந்த ஒன்றுதான். பூமிதான் மையம், அதனைச் சுற்றித்தான் சூரியன், சந்திரன், பிற கோள்கள் என அனைத்தும் செல்கின்றன என்பதை அடிப்படையாகக் கொண்டு டாலமி என்பவர் ஒரு மாதிரியை உருவாக்கியிருந்தார். அதில் கோள்கள் பூமியைச் சுற்றி இப்படிப்பட்ட சைக்ளாய்ட் வடிவில், வளைந்து வளைந்து செல்லும்.

கலீலியோவுக்கும் சைக்ளாய்ட் வடிவம் பற்றி நன்கு தெரிந்திருந்தது. ஆனால், தான் உருவாக்கியிருந்த புதிரின் விடை அதுதான் என்பது அவருக்குத் தெரியவில்லை. சைக்ளாய்ட் வடிவத்தை எடுத்துக்கொண்டு, அதன் ஒரு வளைவின் பரப்பளவு, அதன் நீளம் ஆகியவற்றையெல்லாம் அளக்க அவர் முயற்சி செய்தார். ஆனால், அதற்கான கருவிகள் அவரிடம் இருக்கவில்லை. (கால்குலஸ்தான்!)

கடைசியாக, கால்குலஸை கொஞ்சம் தவறாகப் பயன்படுத்தி, யோஹான் பெர்னோலிதான், இந்த ‘மிகக் குறுகிய நேரத்தில்’ ஒரு புள்ளியிலிருந்து இன்னொரு புள்ளிக்கு வந்துசேர என்ன வடிவம் பயன்படும் என்பதற்கான விடை இந்த ‘சைக்ளாய்ட்’தான் என்பதைக் கண்டுபிடித்தார். பின், இந்தத் துறையின் பிதாமகர்கள் நியூட்டன், லீபினிட்ஸ், யாக்கோப் பெர்னோலி போன்றோர், இதனை உறுதி செய்து, பிழைகளைக் களைந்தனர்.

நாம் சிறுவயதில் டயர் விடும்போது இதையெல்லாம் யோசித்துப் பார்த்திருக்கிறோமா?

கொஞ்சம் டயரை வேறு மாதிரியெல்லாம் விட்டுப் பார்ப்போம். டயர் சமதளத்தில் மீது ஓடாமல், வட்டமான பாதையில் போகிறது என்று வைத்துக்கொள்ளுங்கள். அதாவது ஒரு பெரிய வட்டத்தின் வெளியே, அதனோடு ஒட்டிக்கொண்டு ஒரு சிறிய வட்டமான டயர் சுற்றுகிறது என்று வைத்துக்கொள்ளுங்கள். அப்போதுதான் டாலமி மாதிரி வரும்.

ஒரு பெரிய வட்டத்தின் உள்பக்கம் ஒட்டிக்கொண்டு ஒரு சிறிய வட்டம் சுற்றுகிறது என்று வைத்துக்கொள்ளுங்கள். அப்போது எம்மாதிரியான வடிவங்கள் கிடைக்கும்?

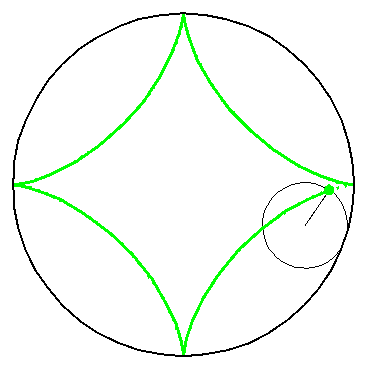
இதனையெல்லாம் நீங்களே செய்து பார்க்கலாம். உங்கள் கை வளையல்கள் போதும். (ஆண்களாக இருந்தால், சகோதரிகளிடமிருந்து சில ரப்பர் வளையல்களைத் தெரியாமல் எடுத்துக்கொள்ளுங்கள்.) சிறிய வட்டங்களை அட்டையில் வெட்டி எடுத்துக்கொள்ளுங்கள். இந்தக் குட்டி வட்டத்தின் ஓரத்தில் ஒரு சிறு ஓட்டையை போட்டு அதில் பென்சில் முனையைச் செருகிக்கொள்ளுங்கள். இப்போது இந்த வட்ட அட்டையை வளையலின் உள்பக்கம் அல்லது வெளிப்பக்கம் ஒட்டியிருக்குமாறு சுற்றுங்கள். பென்சிலால் ஆங்காங்கே அழுத்திப் புள்ளி வைத்துக்கொள்ளுங்கள்.

இது உங்களுக்கு விதவிதமான சைக்ளாய்ட் வடிவங்களைத் தரும்.

இந்த வடிவங்களைக் கொண்ட கியர்களைக் கூடச் செய்துள்ளார்கள்.

நாம் முதலில் பார்த்த சைக்ளாய்டுக்கு (படம் 6) மற்றுமொரு சுவாரசியமான பண்பும் உண்டு. இதற்கு ‘டாட்டோக்ரோன்’ என்று பெயர்.

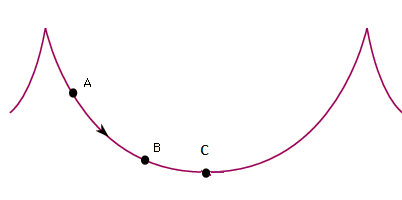
இங்கே, எந்த இடத்தில் ஒரு பொருளை வைத்தாலும், அது புவி ஈர்ப்பு விசையால் இழுக்கப்பட்டு ‘C’ என்ற கீழாக உள்ள இடத்தை அடைய ஒரே அளவு நேரத்தைத்தான் எடுத்துக்கொள்ளும்! (உராய்வு இல்லை என்று வைத்துக்கொள்ளவும்.) அதாவது ‘A’ அல்லது ‘B’ என்று எங்கு பொருளை வைத்தாலும் அது ‘C’-ஐ வந்து அடைய எடுத்துக்கொள்ள ஆகும் நேரம் ஒன்றுதான்!

இதை உள்ளுணர்வால் புரிந்துகொள்வது மிகக் கடினம்! ஆனால், அதுதான் கணிதரீதியாக உங்களுக்குக் கிடைக்கும் பதில்.

பத்ரி சேஷாத்ரி <bseshadri@gmail.com>